Archimede opere e studi
Le opere e gli studi di Archimede







Fra i numerosi manoscritti di Archimede, dopo le vicende del passato, ci sono alla fine pervenute (edizione 1910-1915 con la traduzione di Heiberg) le seguenti opere qui elencate in ordine non cronologico.Le Opere, non in ordine cronologico, sono qui ridotte o appena accennate perché o meno interessanti o vaste e/o con molte problematiche in genere comprensibili con difficoltà solo dopo studi finali nella Scuola Media Superiore: tali Opere, insieme a quelle prima citate nel testo (“Metodi”, “Catapulte” e la “Tecnologia militare”), sono trattati in un’altra e più vasta pubblicazione (citate alla fine della “Premessa”).
Sull’equilibrio dei piani I° e II°
Vi vengono trattati complessivamente i fondamenti della statica geometrica applicati alla meccanica: la legge della leva (ridotta ora ad un segmento con il fulcro in un punto), con i momenti e le condizioni d’equilibrio che, per una leva data, dipendono soltanto dai pesi applicati e dalla posizione dei centri di gravità. Questi ultimi, determinati in generale sull’asse o sul diametro di figure esistenti, vengono trovati in particolare per il triangolo, trapezio, parallelogramma, segmento e tronco di parabola.
Nel periodo ellenistico esistevano già molte macchine, progettate e costruite in serie, composte dal gruppo della leva (come carrucole fisse e mobili, taglie, argani e verricelli) e del piano inclinato (come cunei, viti ottenute con torni, a volte fornite di madrevite, autofilettanti, continue e di precisione). Archimede perfezionando tale tecnologia e sfruttando anche l’invenzione della ruota dentata, utile a trasferire il moto e per ottenere ingranaggi demoltiplicatori, inventò diverse macchine composite (come l’ “Elice”, una vite continua collegata a rocchetti dentati), con dati parametri e vantaggi voluti, che furono impiegate soprattutto nel campo militare per le macchine belliche e le applicazioni navali.
Proprio in occasione di una di queste, dopo il varo di una grande nave reale eseguita da solo ma con i suoi congegni, Archimede esclamò, la frase famosa: “Datemi un punto d’appoggio e vi solleverò il mondo”.
Traduzione latina dei Codici di Archimede (A e B, XIII sec.) Autografo di Moerbeke conservato presso la biblioteca Vaticana.


Francobolli commemorativi: “La sfera e il cilindro”, simbolo delle Opere archimedee, per l’“Anno Mondiale della Matematica”; Archimede, il grande scienziato e inventore, precursore della Scienza d’Europa (raffigurazione erronea ora attribuita ad Archidamo III, re di Sparta).

Macchine archimedee, disegni dell’erudito G.M. Mazzucchelli (metà del XVIII sec.) ispirati dal Codice Atlantico di Leonardo da Vinci.

Sui galleggianti I° e II°
Il famoso e scolastico “Principio”: «un corpo immerso in un liquido (fluido) riceve una spinta verticale dal basso verso l’alto uguale al peso del volume di liquido (fluido) spostato» che Archimede, avrebbe scoperto immerso nel bagno uscendo nudo e urlando più volte “Eùreka”, è in effetti dedotto da Galileo da due Postulati, premessa al I° libro della statica dei liquidi (Meccanica), da cui si possono dedurre anche altri principi come quelli della forma delle superfici grandi e piccole dei liquidi, dei vasi comunicanti e del concetto di “peso specifico” (assoluto e relativo). Fu proprio tale concetto a far risolvere ad Archimede un problema sottopostogli dal Re Gerone II° che aveva dei dubbi sulla purezza dell’oro impiegato in una corona commissionata ad un orafo.
FIG. 10. Archimede scopre l’inganno della corona di Ierone II;
riproduzione di xilografia del tardo medioevo; I protagonisti della civiltà n. 20 pag. 41.

Per scoprire l’inganno bastò calcolare, con una bilancia idrostatica (riutilizzata ancora da Galileo), due pesi uguali d’oro e d’argento nei rapporti con i relativi pesi e/o volumi dell’acqua spostata; poi ripetendo le stesse operazioni con la corona d’oro ottenne un “peso specifico” diverso, minore dell’oro puro e maggiore di quello dell’argento, che gli fece capire subito la frode; per individuare alla fine con precisione anche la percentuale d’oro sottratta, piuttosto che con un calcolo teorico, Archimede avrà probabilmente confrontato il “peso specifico” della corona contraffatta (in lega) con i vari “pesi specifici” di varie percentuali di oro con argento ottenute sperimentalmente.
quadratura della parabola
“Quadrare” una data area significava letteralmente trovarla con un quadrato equivalente calcolato con riga e compasso; un problema a volte non risolvibile come in questo caso. Archimede estende qui la definizione, applicando una possibile dimostrazione euristica-geometrica, ad un poligono equivalente; quindi, in questo caso, significò calcolare col “Metodo meccanico” e geometricamente la misura reale di un segmento di parabola, nel rapporto dei 4/3, con quella di un triangolo di uguale base e altezza.
Quadratura della parabola.

Sulla sfera e il cilindro I° e II°
Archimede volle che fosse ricordata sulla sua tomba, come simbolo delle varie e laboriose Opere, per le complessità dimostrative superate per calcolare la Superficie e il Volume della sfera.
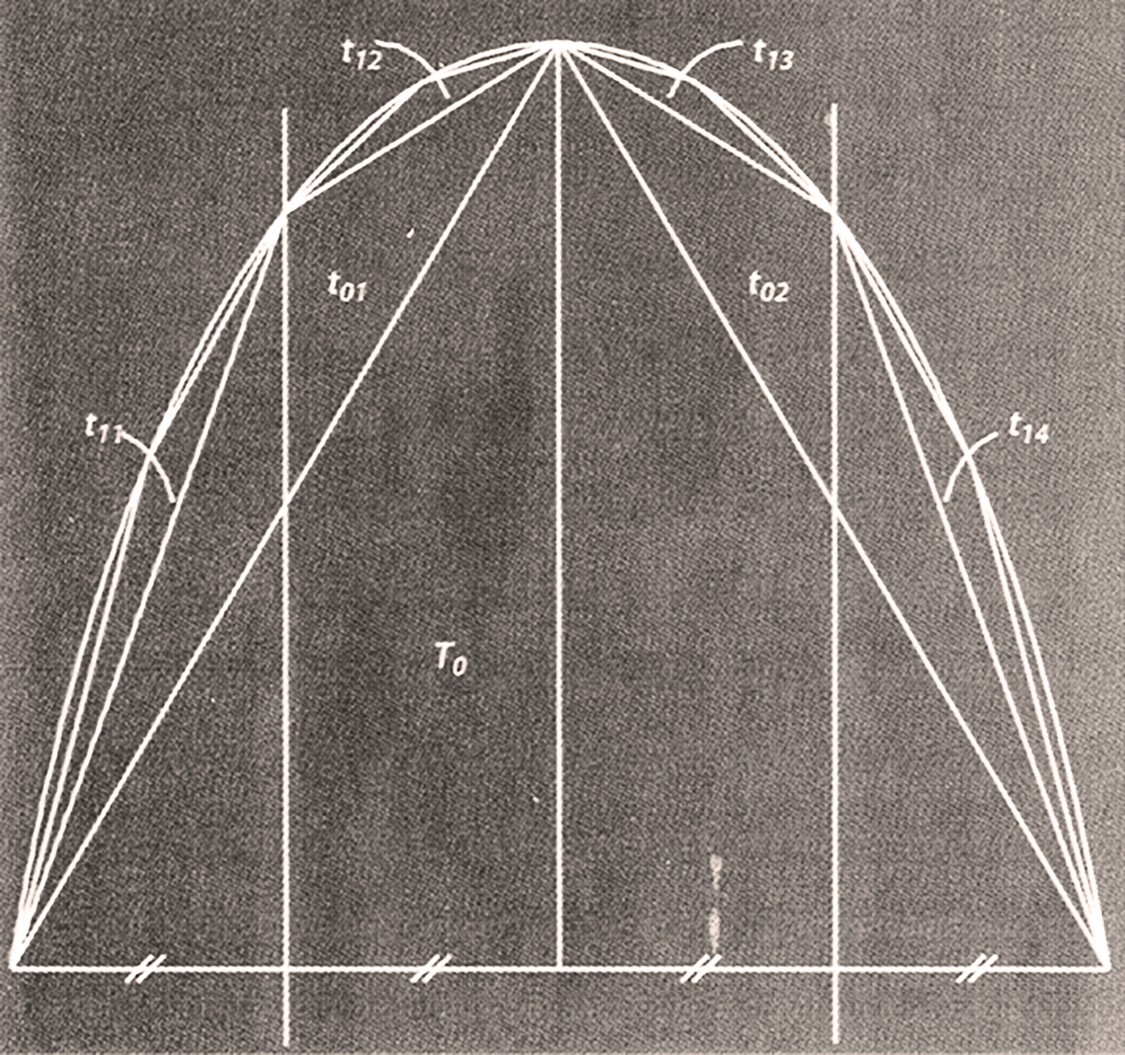
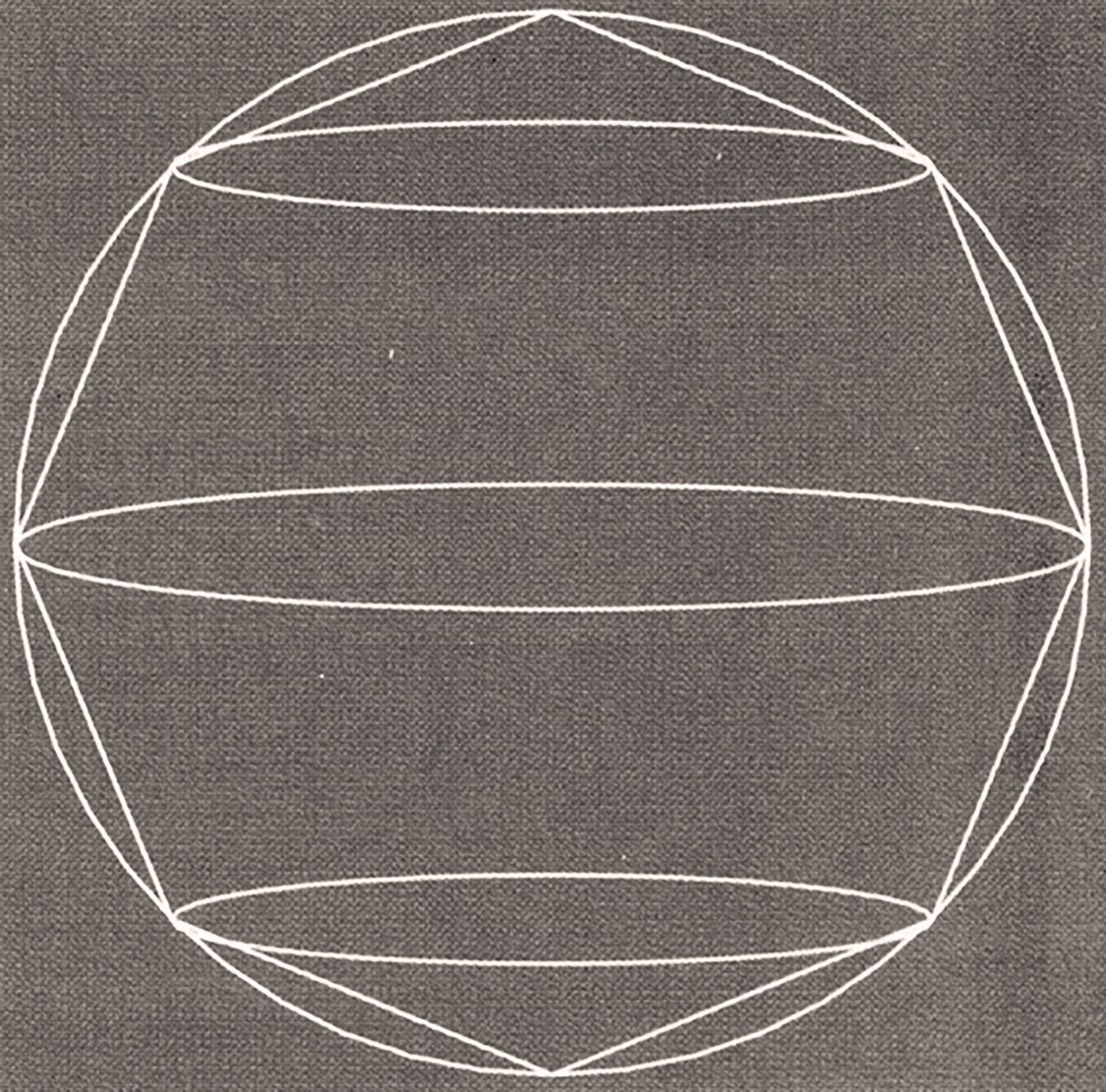
All’inizio, intuendo una tecnica analoga a quella usata nella “Spirale” per “quadrare” con un triangolo il cerchio, stabilisce che il Volume deve essere equivalente a quello di un cono (già calcolato da Eudosso) con altezza e base uguali al raggio e alla superficie del cerchio; quindi facendo ruotare il cerchio con i poligoni approssimanti (usati in precedenza per trovare la circonferenza col Metodo di Esaustione) ottiene una sfera e i relativi solidi approssimanti, somiglianti all’unione di due mezze “mele sbucciate”, composti da coni e tronchi di cono. Per calcolare questi ultimi volumi composti, genialmente e con un complicato apparato dimostrativo ridusse tutto ad una somma di corde sul cerchio massimo della sfera. Così brillantemente trovò che la cercata area di base del cono, fondamentale per il calcolo del suo volume, è uguale a 4 cerchi massimi della sfera.
Concluse poi con una semplice dimostrazione che volume e superficie del cilindro circoscritto alla sfera, cioè con base e altezza uguali al diametro del cerchio massimo, sono equivalenti ai 3/2 di quelli della stessa sfera.
FIG. 12.b La “mela sbucciata”

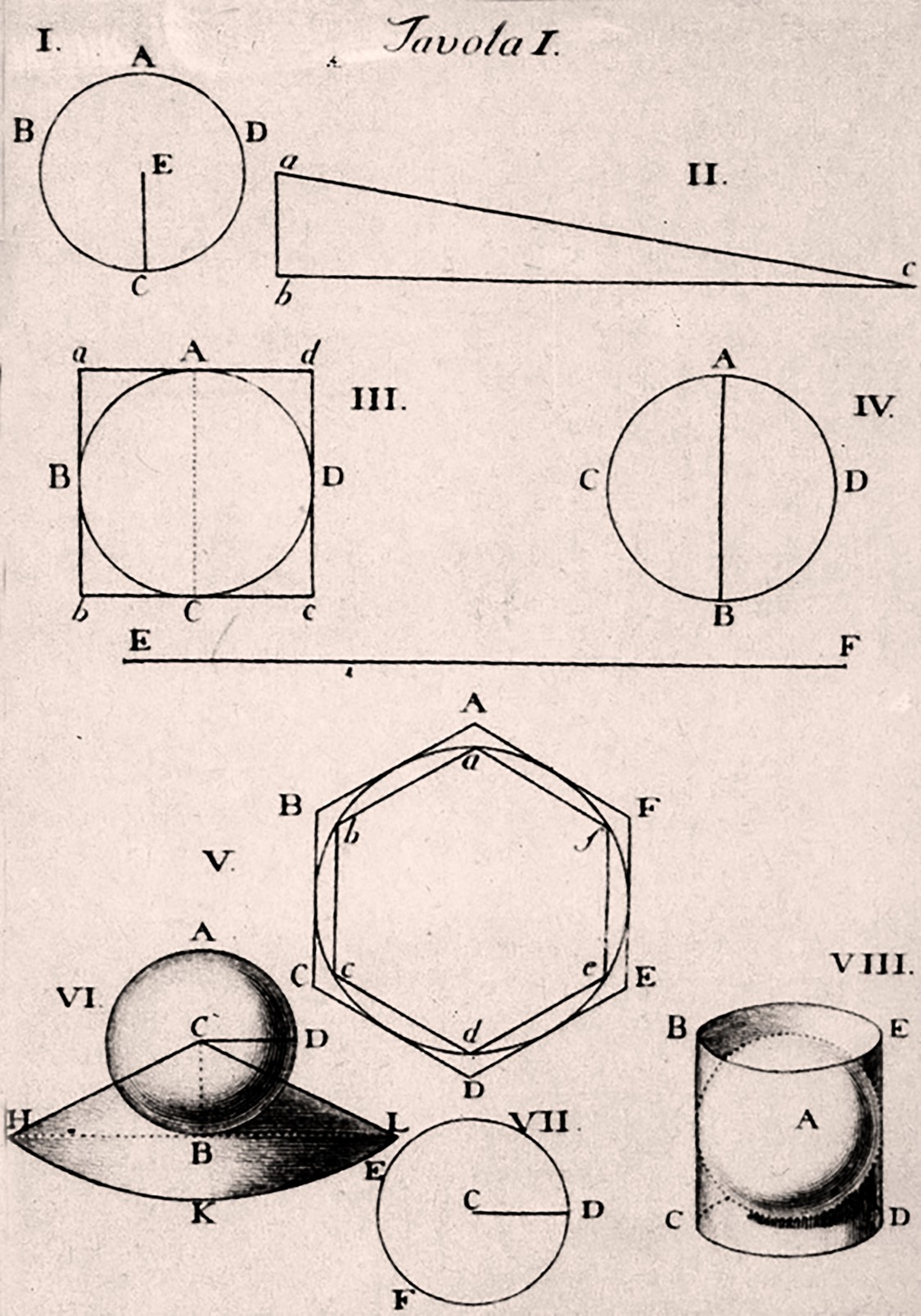
Raffigurazioni archimedee della geometria piana e solida (tavola redatta da G.M. Mazzucchelli - metà del XVIII sec.)

Raffigurazioni archimedee della geometria piana e solida (tavola redatta da G.M. Mazzucchelli - metà del XVIII sec.)

Sui conoidi e gli sferoidi
Opera vasta dove, con lo studio della rotazione di sezioni della superficie laterale di un cono, diversamente inclinata, si calcolano i volumi delle figure ottenute (oltre al cerchio descritto, di parabola, iperbole ed ellisse), trovando i centri di gravità e applicando il Metodo meccanico: tali figure sono oggi chiamate rispettivamente “paraboloide e iperboloide” di rivoluzione, ed “ellissoide.
Con quest’opera tarda lo scienziato (applicando un metodo analogo a quello moderno di “integrazione”) riesce ad arrivare semplicemente alle soluzioni generalizzando le tecniche complicate applicate “Sulla Sfera e il cilindro”.
Libro dei Lemmi
Studi con proposizioni dimostrative e le “quadrature” di particolari e nuove figure geometriche somiglianti ad oggetti comuni, come l’”arbelon” (la “lesina”) e il “salinon” (la “saliera”), ottenibili con intersezioni di semicerchi; viene trattata anche la trisezione dell’angolo con una semplice ma artificiosa costruzione geometrica alla base di un pratico e rapido strumento realizzato nel XVII sec. dal geniale scienziato B. Pascal.
Libro dei Buoi Brevissima opera, come sfida o scherno ai matematici alessandrini, per trovare la soluzione impossibile al paradossale problema di calcolare l’enorme numero di vacche e tori, diversi per razze e colori, che (non) potevano essere tenuti al pascolo in Sicilia dal dio Sole.
Stomachion il curioso “problema che fa impazzire” denominato dai romani quadratum o loculus Archimedis
immagine da Morelli 2009

Era un gioco abbastanza diffuso tra i greci e i romani perché, oltre che divertente era utile al ragionamento matematico e a rinforzare la memoria. Praticamente una specie di “puzzle” che può essere appena paragonato con il moderno gioco, ma solo con sette elementi, del tangram, di antica origine cinese; lo Stomachion aveva una forma quadrata che accoglieva all’interno 14 parti, fra loro commensurabili, costituite da lamelle d’avorio o legno a forma di triangoli, quadrilateri e anche un pentagono, che separate e ricomposte potevano dare origine alle forme più strane e fantastiche in una diversa combinatoria.
Stomachion -ricostruzione congetturale elaborata da Antonio Randazzo

MISURA DEL CERCHIO (TT) E SPIRALE
Prima di Archimede, molti matematici antichi (“sicuri” quelli egiziani almeno dal XVIII sez. a.C.), e poi quelli greci, sino ad Euclide, si erano già occupati di cerchio e circonferenza e avevano già trovato il rapporto tra quest’ultima ed il suo diametro, ma i risultati erano stati grossolani o poco precisi.
Solo il nostro scienziato, introducendo il concetto di numero “irrazionale”, risolse tali problemi in maniera ancora approssimata, essendo le grandezze incommensurabili (cioè con numeri decimali illimitati e non periodici), ma molto più precisa (sino a 15 decimali), poi dimostrata rigorosamente.
Quindi segue il calcolo, col Metodo di Esaustione, della lunghezza della circonferenza come valore “limite” cui tendono i poligoni approssimanti inscritti e circoscritti (ognuno di 96 lati e forse molto di più); infine dimostra che il rapporto fra circonferenza e diametro, preso come unità, il noto -pi greca- = 3,1416 circa (arrotondando praticamente) è in modo molto preciso di 3 volte più diversi decimali compresi fra un valore minore a 10/70 e maggiore a 10/71, valori limite anche dei poligoni approssimanti circoscritti e inscritti alla circonferenza.
Archimede trova anche, probabilmente col Metodo meccanico, che numericamente: “L’area di un cerchio (o di un settore circolare) è uguale a quella di un triangolo rettangolo con i cateti uguali al raggio e alla circonferenza (o all’arco di settore)”.
Nella seconda Opera “Sulla Spirale” si parla appunto dello studio delle spirali, delle loro proprietà e dei rapporti verificanti tra la più semplice spirale con il cerchio e la circonferenza.
La prima e più semplice delle linee spirali è quella studiata da Archimede (e che porta quindi il suo nome) nella lunga e difficile opera “Sulle Spirali” interpretata con sicurezza solo nel XVII° sec. dal gesuita Bonaventura Cavalieri, amico e allievo di Galileo.
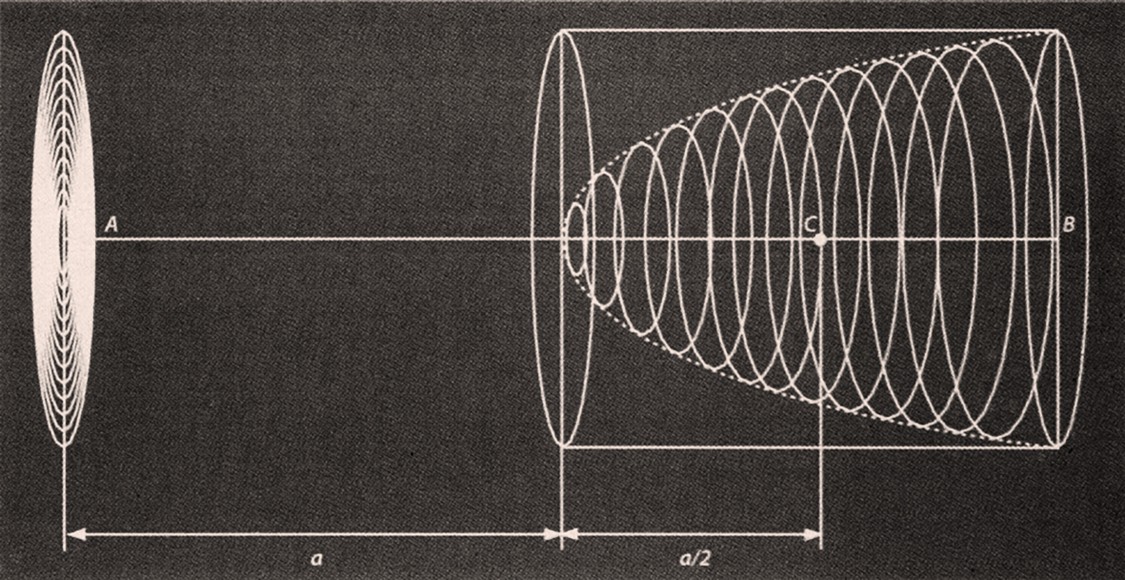
Il matematico siracusano definì la sua spirale con la commistione di argomenti geometrici e “cinematici”originali (composizione di moti uniformi, circolare e rettilineo): <<Se una linea retta (o segmento) rimanendo fermo un estremo, viene fatta ruotare nel piano con velocità costante fino a farla tornare di nuovo nella posizione di partenza, e insieme con la retta ruotante viene mosso un punto sulla retta con velocità costante cominciando dall’estremo fisso, il punto descrive nel piano una spirale>>.
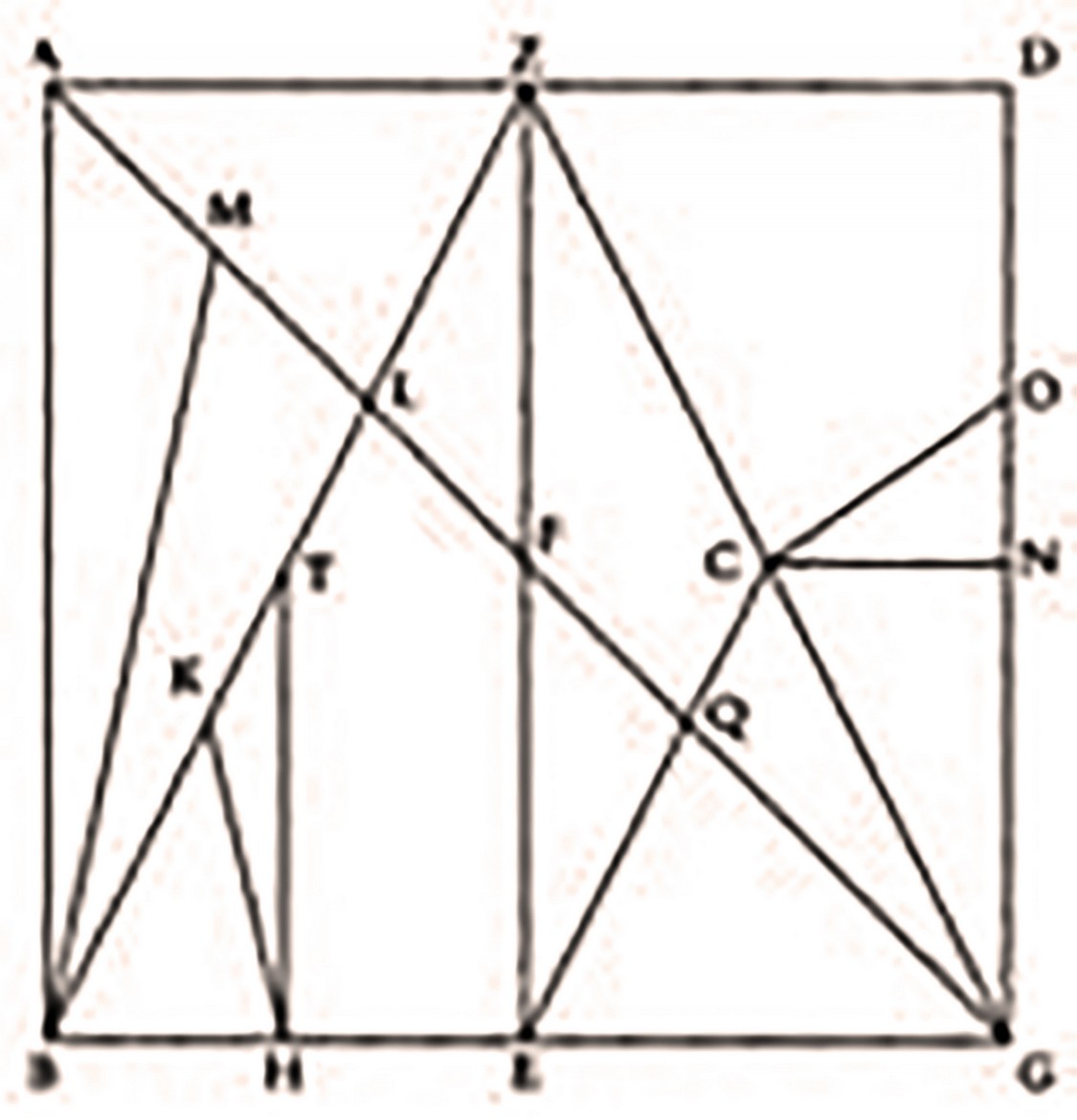
I risultati più interessanti dello studio di questa spirale, dopo una prima rotazione, sono due: la superfice della Spirale descritta è 1/3 di quella del cerchio circoscritto; aver poi ottenuto e dimostrato, con una successiva costruzione geometrica (in figura) che il segmento trovato, intersezione fra la perpendicolare abbassata dal centro e la sottotangente alla Spirale, rappresenta la rettificazione vera e propria della circonferenza.
Spirale e cerchio

L’“ARENARIO” E L’ASTRONOMIA (LA “SFERA”)
Archimede fu affascinato sin da ragazzo dall’Astronomia inculcatagli, come già detto, con la connessa Matematica dal padre Fidia; sviluppando i suoi studi alessandrini, dove fu, come detto, molto influenzato dalla frequentazione di grandi astronomi (come Ipparco da Rodi, Eratostene di Cirene, e Aristarco di Samo), fece numerosi studi e scoperte (misure del Sole, Terra, Luna, ecc…) che lasciano sospettare l’aiuto del cannocchiale a riflessione da lui inventato.
Una delle opere del nostro Scienziato, “ARENARIO”, è soprattutto uno studio di tipo aritmetico per le suddette scoperte astronomiche dove si dimostra come si possa contare (anticipando il concetto di logaritmo) persino il numero dei granelli di sabbia contenuti nell’Universo; ciò consentì finalmente ai greci di poter eseguire, con la serie dei numeri naturali, nuovi calcoli anche infinitamente grandi come quelli astronomici.
Si attribuisce quindi ad Archimede, come conseguenza dei suoi studi, la costruzione di uno strumento meccanico in rame protetto da un globo di vetro che per la sua forma fu chiamato “la SFERA”, un vero e proprio planetario che, ora meccanicamente perfetto rispetto a quelli più antichi, per primo riproduceva e spiegava didatticamente, con le eclissi della terra, le “apparenze” dei moti del sole, della luna e dei pianeti allora conosciuti (solo cinque).
Alcuni esemplari della “Sfera”, in grande considerazione presso gli antichi, furono poi trasportate, come bottino di guerra da Siracusa a Roma: una fu posta sul tempio della Virtù militare (o di Vesta) ma nulla è giunto fino a noi.
FIG. 15. Copia ellenistica (II° sec. a.C., ora al Museo Archeologico Nazionale di Napoli) saccheggiata in Asia minore e portata da Lucello a Roma: la statua in marmo rappresenta il gigante Atlante che sostiene il cielo con le costellazioni che sono finemente scolpite e che avvolgono il sistema solare la “Sfera”di Archimede.

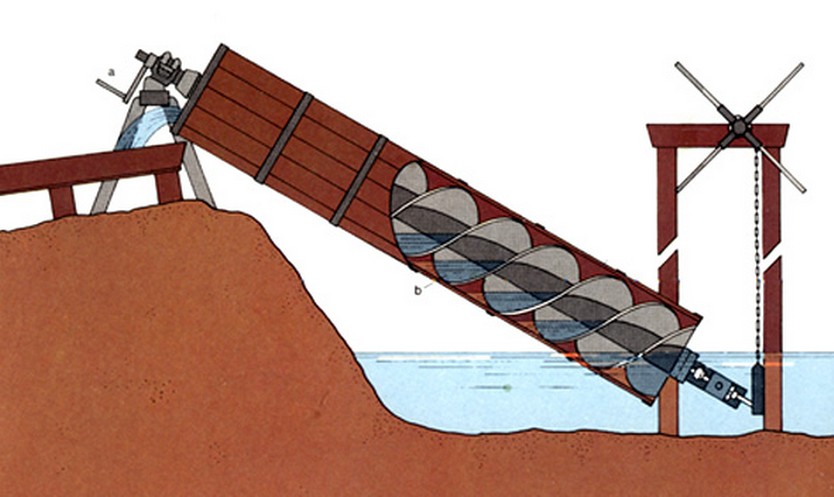
la Coclea

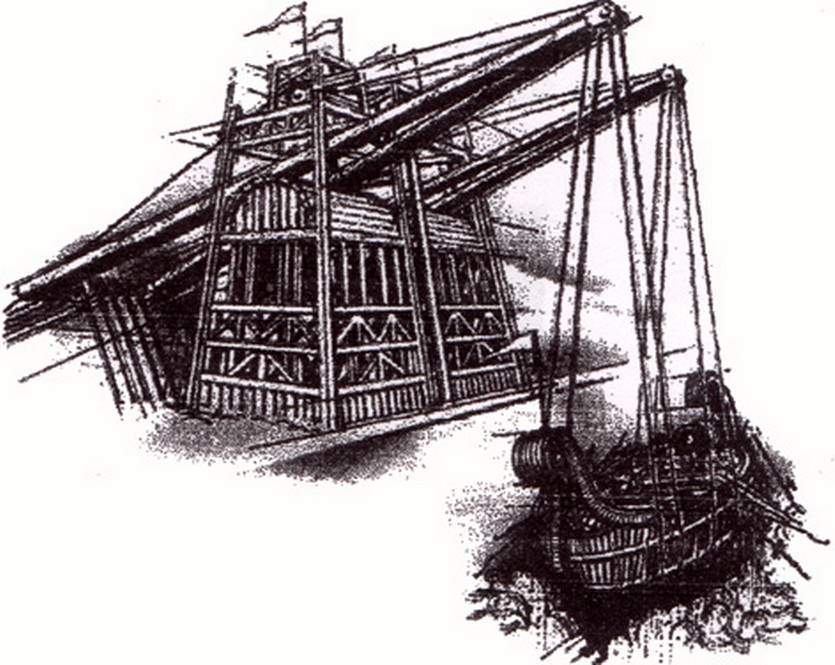
Manus ferrea

Testi di Roberto Mirisola con la collaborazione di Antonio Randazzo
BIBLIOGRAFIA
Diodoro Siculo, BIBLIOTHECA HISTORICA, XX, XCI, 1-6;
Polibio, HISTORIAE, VIII, 7-9;
Livio, AB URBE CONDITA, libro XXI;
Plutarco, VITA MARCELLI, XV, 1-3;
Silio Italico, PUNICA ( assedio di Siracusa);
Cicerone, DE REPUBLICA, I, XIV (21-22); TUSCULANEA, V, XXXIII (64-66);
DE NATURA DEORUM, II, XXXIV (87-88);
AA. VV., Siracusa ellenistica; Catanzaro 1997;
P.Bertezzolo, ARCHIMEDE; Verona 1981;
G. Cavallo, et alii, LE BIBLIOTECHE NEL MONDO ANTICO E MEDIEVALE;
Roma-Bari 1988;
C. Dollo, curatore, ARCHIMEDE: Mito, tradizione, scienza; Firenze 1992;
A. Frajese, ARCHIMEDE; Torino 1974;
E. Garin, IL RITORNO DEI CLASSICI ANTICHI; Napoli 1984;
P. Midolo, ARCHIMEDE e il suo tempo;Siracusa 1912 (Rist. Ed. A. Lombardi,
SR 1989);
P.D. Napolitani, ARCHIMEDE; Le Scienze n.22, Milano 2001;
B. Pace, LA NAVE DI GERONE; Palermo 1912;
L. Polacco e R. Mirisola, L’ACROPOLI E IL PALAZZO DEI TIRANNI
NELL’ANTICA SIRACUSA; Venezia 1999;
P. Lawrence Rose, THE ITALIAN RENAISSANCE OF MATHEMATICS; Dror 1976;
L Russo, LA RIVOLUZIONE DIMENTICATA; Milano 2001;
E. Zucher, LA MECANIQUE D’ANTICYTHERE, (pp. 54-60 e 89-91); IPAAM, Nice 2004.
N.B. si è anche tenuto conto delle notizie fornite dall’Ing. Umberto Di Marco
nella interessante Conferenza (Armi da getto ellenistiche e strategie per la
fortezza del “Castello” Eurialo), tenuta per la Società Siracusana di Storia Patria,
il 25-05-2004, presso il Palazzo Impellizzeri di Siracusa.
Foto, grafica, elaborazione, impaginazione e stampa: Antonio Randazzo
Siracusa aggiornamento Luglio 2000
